Chương 1: Logic - Tập hợp
+5
nguyenhuuduc08(k19)
huynhleanhtuank19
NgoTrungHieu16050054
nguyenkhaminhtri
Admin
9 posters
Trang 1 trong tổng số 1 trang
Chương 1: Logic - Tập hợp
Admin 6/2/2017, 13:29
Kiến thức cơ sở: Logic và Tập hợp !
Thảo luận những vấn đề liên quan.
Thảo luận những vấn đề liên quan.
Admin- Admin
- Tổng số bài gửi : 294
Join date : 18/02/2009 -
Bảng Kí Tự trong Toán Rời Rạc
nguyenkhaminhtri 22/2/2017, 07:59
ALT + 26 = →
ALT + 29 = ↔
ALT + 170 = ¬
ALT + 0136 = ^
ALT + 118 = v
Admin:
- Có cố gắng !
- Tuy nhiên, cần kiểm tra lại các tổ hợp phím trên đã chuẩn chưa, mặc dù ký hiệu logic tương ứng có dáng vẻ đúng.
- Nên thêm câu giải thích thêm, vì như trên quá "trần trụi", hơi "lười".
ALT + 29 = ↔
ALT + 170 = ¬
ALT + 0136 = ^
ALT + 118 = v
Admin:
- Có cố gắng !
- Tuy nhiên, cần kiểm tra lại các tổ hợp phím trên đã chuẩn chưa, mặc dù ký hiệu logic tương ứng có dáng vẻ đúng.
- Nên thêm câu giải thích thêm, vì như trên quá "trần trụi", hơi "lười".
nguyenkhaminhtri- Tổng số bài gửi : 2
Join date : 16/02/2017
Lập bảng chân trị chứng minh 2 biểu thức tương đương
PhanTanSangK19 23/2/2017, 00:34
Lấy ví dụ của thầy:
Bạn không được lái xe máy nếu bạn cao dưới 1,5m trừ khi bạn 18 tuổi.
Đặt:
q là mệnh đề "bạn được lái xe máy
r là mệnh đề "bạn cao dưới 1,5m"
s là mệnh đề "bạn trên 18 tuổi"
Chứng minh ( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s )
Ta có bảng chân trị
Từ bảng chân trị trên, ta thấy, với mọi tổ hợp giá trị T và F của 3 mệnh đề q, r, s thì đều cho ra kết quả của hai mệnh đề q → (¬r V s ) và ( r Ʌ ¬s ) → ¬q là cùng T hoặc cùng F.
=> ( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s ) (Đpcm)
Admin:
- Rất tốt !
- Hướng dẫn các bạn nhập được các ký hiệu logic như đã làm !
- Đây là Cách chứng minh thứ 1, còn Cách 2 thế nào?
Bạn không được lái xe máy nếu bạn cao dưới 1,5m trừ khi bạn 18 tuổi.
Đặt:
q là mệnh đề "bạn được lái xe máy
r là mệnh đề "bạn cao dưới 1,5m"
s là mệnh đề "bạn trên 18 tuổi"
Chứng minh ( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s )
Ta có bảng chân trị
Từ bảng chân trị trên, ta thấy, với mọi tổ hợp giá trị T và F của 3 mệnh đề q, r, s thì đều cho ra kết quả của hai mệnh đề q → (¬r V s ) và ( r Ʌ ¬s ) → ¬q là cùng T hoặc cùng F.
=> ( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s ) (Đpcm)
Admin:
- Rất tốt !
- Hướng dẫn các bạn nhập được các ký hiệu logic như đã làm !
- Đây là Cách chứng minh thứ 1, còn Cách 2 thế nào?
PhanTanSangK19- Tổng số bài gửi : 10
Join date : 16/02/2017
Re: Lập bảng chân trị chứng minh hai biểu thức tương đương
PhanTanSangK19 23/2/2017, 09:36
Bài toán chứng minh hai biểu thức tương đương, ở cách 1 (dùng bảng chân trị) , em đã sửa lại theo góp ý của thầy.
Và bổ sung:
Cách 2 (Dùng các định luật và các biểu thức đã biết):
Chứng minh:
( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s )
Áp dụng: p → q ≡ ¬q → ¬p
("Kéo theo" tương đương với "Phản đảo" của nó)
Ta có:
Vế trái ≡ ¬¬q → ¬( r Ʌ ¬s )
≡ q → ¬( r Ʌ ¬s )
≡ q → (¬r V ¬¬s ) (Áp dụng Định luật De Morgan)
≡ q → (¬r V s ) = Vế phải
(*) Định luật De Morgan: Phủ định của một hội bằng tuyển các phủ định.
(Admin: Rất nhớ câu này của thày !)
____________________
Cách nhập các kí hiệu logic:
Cách 1: Dùng Insert > Symbol trong Office. (Thầy đã nêu)
Cách 2: Dùng cách bấm tổ hợp Alt + Số (như của bạn Trí).
Bổ sung: Cách của bạn Trí tuy nhanh nhưng yêu cầu phải nhớ mã của từng kí hiệu. Mặt khác, cách của bạn Trí chỉ sự dụng được trên những máy tính có bàn phím full size (Có bàn phím số riêng bên trái). Mình bổ sung thêm cách nhập kí hiệu logic có thể áp dụng trên nhiều dòng máy (Kể cả những máy không cài office và máy không có bàn phím số riêng)
Dùng Character map
Đầu tiên gõ character map trong cửa sổ windows, rồi mở tiện ích character map.
-Trong ô font chọn Arial
-Tìm và kí hiệu logic cần nhập và paste vào nơi cần paste.
p/s: Để cho nhanh, copy tất cả các kí tự logic vào Notepad và lưu ngoài desktop để khi nào dùng thì mở lên copy cho nhanh.
Và bổ sung:
Cách 2 (Dùng các định luật và các biểu thức đã biết):
Chứng minh:
( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s )
Áp dụng: p → q ≡ ¬q → ¬p
("Kéo theo" tương đương với "Phản đảo" của nó)
Ta có:
Vế trái ≡ ¬¬q → ¬( r Ʌ ¬s )
≡ q → ¬( r Ʌ ¬s )
≡ q → (¬r V ¬¬s ) (Áp dụng Định luật De Morgan)
≡ q → (¬r V s ) = Vế phải
(*) Định luật De Morgan: Phủ định của một hội bằng tuyển các phủ định.
(Admin: Rất nhớ câu này của thày !)
____________________
Cách nhập các kí hiệu logic:
Cách 1: Dùng Insert > Symbol trong Office. (Thầy đã nêu)
Cách 2: Dùng cách bấm tổ hợp Alt + Số (như của bạn Trí).
Bổ sung: Cách của bạn Trí tuy nhanh nhưng yêu cầu phải nhớ mã của từng kí hiệu. Mặt khác, cách của bạn Trí chỉ sự dụng được trên những máy tính có bàn phím full size (Có bàn phím số riêng bên trái). Mình bổ sung thêm cách nhập kí hiệu logic có thể áp dụng trên nhiều dòng máy (Kể cả những máy không cài office và máy không có bàn phím số riêng)
Dùng Character map
Đầu tiên gõ character map trong cửa sổ windows, rồi mở tiện ích character map.
-Trong ô font chọn Arial
-Tìm và kí hiệu logic cần nhập và paste vào nơi cần paste.
p/s: Để cho nhanh, copy tất cả các kí tự logic vào Notepad và lưu ngoài desktop để khi nào dùng thì mở lên copy cho nhanh.
PhanTanSangK19- Tổng số bài gửi : 10
Join date : 16/02/2017
bài tập chứng minh tương đương
levanhung 23/2/2017, 11:55
Để chứng minh hai biểu thức : r ٨¬s →¬ q ≡ q→ ¬r ٧ s
*Ta có hai cách:
* CÁCH 1: Ta chứng minh hai biểu thức tương đương vs nhau bằng bảng sự thật:
Ta đã chứng minh xong! Đó là cách 1
*CÁCH 2
Ta sử dụng mệnh đề De Mocgan như sau
p → q ≡ ¬q→ ¬p
Admin: Đây không phải là Luật De Morgan!
đầu tiên chứng minh biểu thức trên bằng bảng sự thật:
Ta đã chứng minh được biểu thức trên tương đương
Tiếp theo:
Áp dụng tương đương trên ta có:
¬¬q→ ¬(r ٨¬s)
≡ q → ¬(r ٨ ¬s)
≡ q → ( ¬r ٧¬¬s)
≡ q → ( ¬r ٧s )≡ ¬q → (r ٧ ¬s)
Giải thích:
Vì "Phủ định của hội bằng tuyển các phủ định" nên ta có cách chuyển đổi như trên.
Admin:
- Rất cố gắng. Quan trọng là bằng sức của mình (thấy rõ)
- "Phủ định của một hội bằng tuyển các phủ định" mới là Luật De Morgan: ¬(p ٨ q) ≡ (¬p ٧ ¬q)
*Ta có hai cách:
* CÁCH 1: Ta chứng minh hai biểu thức tương đương vs nhau bằng bảng sự thật:
R | S | Q | R ٨ ¬S | ¬R ٧ S | BT1 | BT2 |
T | T | T | F | T | T | T |
T | T | F | F | T | T | T |
T | F | T | T | F | F | F |
T | F | F | T | F | T | T |
F | F | F | F | T | T | T |
F | F | T | F | T | T | T |
F | T | F | F | T | T | T |
F | T | T | F | T | T | T |
Ta đã chứng minh xong! Đó là cách 1
*CÁCH 2
Ta sử dụng mệnh đề De Mocgan như sau
p → q ≡ ¬q→ ¬p
Admin: Đây không phải là Luật De Morgan!
đầu tiên chứng minh biểu thức trên bằng bảng sự thật:
q | p | ¬q | ¬p | p→q | ¬q→¬p |
T | T | F | F | T | T |
T | F | F | T | T | T |
F | F | T | T | T | T |
F | T | T | F | F | F |
Ta đã chứng minh được biểu thức trên tương đương
Tiếp theo:
Áp dụng tương đương trên ta có:
¬¬q→ ¬(r ٨¬s)
≡ q → ¬(r ٨ ¬s)
≡ q → ( ¬r ٧¬¬s)
≡ q → ( ¬r ٧s )≡ ¬q → (r ٧ ¬s)
Giải thích:
Vì "Phủ định của hội bằng tuyển các phủ định" nên ta có cách chuyển đổi như trên.
Admin:
- Rất cố gắng. Quan trọng là bằng sức của mình (thấy rõ)
- "Phủ định của một hội bằng tuyển các phủ định" mới là Luật De Morgan: ¬(p ٨ q) ≡ (¬p ٧ ¬q)
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
TIỀU LIỆU THAM KHẢO
levanhung 23/2/2017, 20:30
Trong phép tính mệnh đề, người ta không quan tâm đến ý nghĩa của câu phát biểu mà chỉ chú ý đến chân trị của các mệnh đề. Do đó, khi thực hiện các phép toán mệnh đề thông thường người ta không ghi rõ các câu phát biểu mà chỉ ghi ký hiệu. Các chữ cái sẽ được dùng để ký hiệu các mệnh đề. Những chữ cái thường dùng là P, Q, R,.....
Mệnh đề chỉ có một giá trị đơn (luôn đúng hoặc sai) được gọi là mệnh đề nguyên từ ( atomic proposition ). Các mệnh đề không phải là mệnh đề nguyên từ được gọi là mệng đề phức hợp (compound propositions). Thông thường, tất cả mệnh đề phức hợp là mệnh đề liên kết (có chứa phép tính mệnh đề).
Các phép tính mệnh đề được sử dụng nhằm mục đích kết nối các mệnh đề lại với nhau tạo ra một mệnh đề mới. Các phép toán mệnh đề được trình bày trong chương này bao gồm : phép phủ định, phép hội, phép tuyển, phép XOR, phép kéo theo, phép tương đương.
Phép phủ định (NEGATION)
Cho P là một mệnh đề, câu "không phải là P" là một mệnh đề khác được gọi là phủ định của mệnh đề P. Kí hiệu : ¬ P (
¯
P
).
Ví dụ : P = " 2 > 0 "
¬ P = " 2 ≤ 0 "
Bảng chân trị (truth table)
p ¬ p
T F
F T
Qui tắc: Nếu P có giá trị là T thì phủ định P có giá trị là F.
Phép hội (CONJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P và Q" là một mệnh đề mới được gọi là hội của 2 mệnh đề P và Q. Kí hiệu P ^ Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P ^ Q = " 2> 0 và 2 = 0 " là mệnh đề sai.
Bảng chân trị
p q p^q
T T T
T F F
F T F
F F F
Qui tắc : Hội của 2 mệnh đề chỉ đúng khi cả hai mệnh đề là đúng. Các trường hợp còn lại là sai.
Phép tuyển (DISJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P hay (hoặc) Q" là một mệnh đề mới được gọi là tuyển của 2 mệnh đề P và Q. Kí hiệu P V Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P V Q = " 2 ≥ 0 " là mệnh đề đúng.
p q pvq
T T T
T F T
F T T
F F F
Bảng chân trị
Qui tắc : Tuyển của 2 mệnh đề chỉ sai khi cả hai mệnh đề là sai. Các trường hợp còn lại là đúng.
Phép XOR
Cho hai mệnh đề P và Q. Câu xác định "loại trừ P hoặc lọai trừ Q", nghĩa là "hoặc là P đúng hoặc Q đúng nhưng không đồng thời cả hai là đúng" là một mệnh đề mới được gọi là P xor Q. Kí hiệu P ⊕ Q.
Bảng chân trị
p q p ⊕q
T T F
T F T
F T T
F F F
Phép toán trên bit
Các máy tính dùng các bit để biểu diễn thông tin. Một bit có 2 giá trị khả dĩ là 0 và 1. Bit cũng có thể được dùng để biểu diễn chân trị. Thường người ta dùng bit 1 để biểu diễn chân trị đúng và bit 0 để biểu diễn chân trị sai. Các phép toán trên bit trong máy tính là các phép toán logic. Thông tin thường được biển diễn bằng cách dùng các xâu bit. Ta có định nghĩa xâu bit như sau:
Định nghĩa : Một xâu bit (hoặc xâu nhị phân) là dãy có một hoặc nhiều bit. Chiều dài của xâu là số các bit trong xâu đó.
Ví dụ : 101011000 là một xâu bit có chiều dài là 9
Có thể mở rộng các phép toán trên bit tới các xâu bit. Người ta định nghĩa các OR bit, AND bit và XOR bit đối với 2 xâu bit có cùng chiều dài là các xâu có các bit của chúng là ca1c OR, AND, XOR của các bit tương ứng trong 2 xâu tương ứng. Chúng ta cũng dùng các kí hiệu ^, v, ⊕ để biểu diễn các phép tính OR bit, AND và XOR tương ứng.
Ví dụ : Tìm OR bit, AND bit và XOR bit đối với 2 xâu sau đây (mỗi xâu được tách thành 2 khối, mỗi khối có 5 bit cho dễ đọc)
01101 10110
11000 11101
11101 11111 OR bit
01000 10100 AND bit
10101 01011 XOR bit
Phép kéo theo (IMPLICATION)
Cho P và Q là hai mệnh đề. Câu "Nếu P thì Q" là một mệnh đề mới được gọi là mệnh đề kéo theo của hai mệnh đề P,Q. Kí hiệu P → Q. P được gọi là giả thiết và Q được gọi là kết luận.
Ví dụ : Cho hai mệnh đề P và Q như sau
P = " tam giác T là đều "
Q = " tam giác T có một góc bằng 60°"
Để xét chân trị của mệnh đề P → Q, ta có nhận xét sau :
- Nếu P đúng, nghĩa là tam giác T là đều thì rõ ràng rằng P → Q là đúng.
- Nếu P sai, nghĩa là tam giác T không đều và cũng không là cân thì dù Q là đúng hay sai thì mệnh đề P → Q vẫn đúng.
Sau đây là bảng chân trị của ví dụ và cũng là bảng chân trị của mệnh đề P →Q.
Qui tắc : mệnh đề kéo theo chỉ sai khi giả thiết đúng và kết luận sai. Các trường hợp khác là đúng.
Từ mệnh đề P → Q, chúng ta có thể tạo ra các mệnh đề kéo theo khác như là mệnh đề Q → P và ¬ Q → P được gọi là mệnh đề đảo và mệnh đề phản đảo của mệnh đề P → Q.
Ví dụ : Tìm mệnh đề đảo và phản đảo của mệnh đề sau
" Nếu tôi có nhiều tiền thì tôi mua xe hơi"
Mệnh đề đảo là :
" Nếu tôi mua xe hơi thì tôi có nhiều tiền"
Mệnh đề phản đảo là :
" Nếu tôi không mua xe hơi thì tôi không có nhiều tiền"
Phép tương đương (BICONDITIONAL)
Cho P và Q là hai mệnh đề. Câu "P nếu và chỉ nếu Q" là một mệnh đề mới được gọi là P tương đương Q. Kí hiệu P Q. Mệnh đề tương đương là đúng khi P và Q có cùng chân trị.
P Q = (P → Q) ^ (Q → P)
Đọc là : P nếu và chỉ nếu Q
P là cần và đủ đối với Q
Nếu P thì Q và ngược lại
Bảng chân trị
p q p ↔q
T T T
T F F
F T F
F F T
Biểu thức mệnh đề (LOGICAL CONNECTIVES)
Cho P, Q, R,... là các mệnh đề. Nếu các mệnh đề này liên kết với nhau bằng các phép toán thì ta được một biểu thức mệnh đề.
Chú ý : . Một mệnh đề cũng là một biểu thức mệnh đề
. Nếu P là một biểu thức mệnh đề thì P cũng là biểu thức mệnh đề
Chân trị của biểu thức mệnh đề là kết quả nhận được từ sự kết hợp giữa các phép toán và chân trị của các biến mệnh đề.
Ví dụ : Tìm chân trị của biểu thức mệnh đề ¬ P ^V (Q ^ R )
Do biểu thức mệnh đề là sự liên kết của nhiều mệnh đề bằng các phép toán nên chúng ta có thể phân tích để biểu diễn các biểu thức mệnh đề này bằng một cây mệnh đề.
Ví dụ : Xét câu phát biểu sau :
" Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả."
Đây là một biểu thức mệnh đề và phép toán chính là phép hội. Có thể viết lại như sau :
"Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có.
Nhưng,
nếu cô ta không thắng thì cô ta sẽ mất tất cả. "
Cả hai mệnh đề chính trong biểu thức mệnh đề này là mệnh đề phức hợp. Có thể định nghĩa các biến mệnh đề như sau:
P: Michelle thắng trong kỳ thi Olympic
Q: mọi người sẽ khâm phục cô ấy
R: cô ta sẽ trở nên giàu có
S: cô ta sẽ mất tất cả
Biểu diễn câu phát biểu trên bằng các mệnh đề và các phép toán, ta có biểu thức mệnh đề sau : ( P → (Q ^ R)) ^ ( ¬ P → S)
Biểu diễn câu phát biểu trên thành một cây ngữ nghĩa như sau :
Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả. Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nếu cô ta không thắng thì cô ta sẽ mất tất cả. AND Michelle thắng trong kỳ thi Olympic Mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Cô ta không thắng Cô ta sẽ mất tất cả. Mọi người sẽ khâm phục cô ấy Cô ta sẽ trở nên giàu có. Cô ta sẽ mất tất cả. AND NOT
Mệnh đề chỉ có một giá trị đơn (luôn đúng hoặc sai) được gọi là mệnh đề nguyên từ ( atomic proposition ). Các mệnh đề không phải là mệnh đề nguyên từ được gọi là mệng đề phức hợp (compound propositions). Thông thường, tất cả mệnh đề phức hợp là mệnh đề liên kết (có chứa phép tính mệnh đề).
Các phép tính mệnh đề được sử dụng nhằm mục đích kết nối các mệnh đề lại với nhau tạo ra một mệnh đề mới. Các phép toán mệnh đề được trình bày trong chương này bao gồm : phép phủ định, phép hội, phép tuyển, phép XOR, phép kéo theo, phép tương đương.
Phép phủ định (NEGATION)
Cho P là một mệnh đề, câu "không phải là P" là một mệnh đề khác được gọi là phủ định của mệnh đề P. Kí hiệu : ¬ P (
¯
P
).
Ví dụ : P = " 2 > 0 "
¬ P = " 2 ≤ 0 "
Bảng chân trị (truth table)
p ¬ p
T F
F T
Qui tắc: Nếu P có giá trị là T thì phủ định P có giá trị là F.
Phép hội (CONJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P và Q" là một mệnh đề mới được gọi là hội của 2 mệnh đề P và Q. Kí hiệu P ^ Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P ^ Q = " 2> 0 và 2 = 0 " là mệnh đề sai.
Bảng chân trị
p q p^q
T T T
T F F
F T F
F F F
Qui tắc : Hội của 2 mệnh đề chỉ đúng khi cả hai mệnh đề là đúng. Các trường hợp còn lại là sai.
Phép tuyển (DISJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P hay (hoặc) Q" là một mệnh đề mới được gọi là tuyển của 2 mệnh đề P và Q. Kí hiệu P V Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P V Q = " 2 ≥ 0 " là mệnh đề đúng.
p q pvq
T T T
T F T
F T T
F F F
Bảng chân trị
Qui tắc : Tuyển của 2 mệnh đề chỉ sai khi cả hai mệnh đề là sai. Các trường hợp còn lại là đúng.
Phép XOR
Cho hai mệnh đề P và Q. Câu xác định "loại trừ P hoặc lọai trừ Q", nghĩa là "hoặc là P đúng hoặc Q đúng nhưng không đồng thời cả hai là đúng" là một mệnh đề mới được gọi là P xor Q. Kí hiệu P ⊕ Q.
Bảng chân trị
p q p ⊕q
T T F
T F T
F T T
F F F
Phép toán trên bit
Các máy tính dùng các bit để biểu diễn thông tin. Một bit có 2 giá trị khả dĩ là 0 và 1. Bit cũng có thể được dùng để biểu diễn chân trị. Thường người ta dùng bit 1 để biểu diễn chân trị đúng và bit 0 để biểu diễn chân trị sai. Các phép toán trên bit trong máy tính là các phép toán logic. Thông tin thường được biển diễn bằng cách dùng các xâu bit. Ta có định nghĩa xâu bit như sau:
Định nghĩa : Một xâu bit (hoặc xâu nhị phân) là dãy có một hoặc nhiều bit. Chiều dài của xâu là số các bit trong xâu đó.
Ví dụ : 101011000 là một xâu bit có chiều dài là 9
Có thể mở rộng các phép toán trên bit tới các xâu bit. Người ta định nghĩa các OR bit, AND bit và XOR bit đối với 2 xâu bit có cùng chiều dài là các xâu có các bit của chúng là ca1c OR, AND, XOR của các bit tương ứng trong 2 xâu tương ứng. Chúng ta cũng dùng các kí hiệu ^, v, ⊕ để biểu diễn các phép tính OR bit, AND và XOR tương ứng.
Ví dụ : Tìm OR bit, AND bit và XOR bit đối với 2 xâu sau đây (mỗi xâu được tách thành 2 khối, mỗi khối có 5 bit cho dễ đọc)
01101 10110
11000 11101
11101 11111 OR bit
01000 10100 AND bit
10101 01011 XOR bit
Phép kéo theo (IMPLICATION)
Cho P và Q là hai mệnh đề. Câu "Nếu P thì Q" là một mệnh đề mới được gọi là mệnh đề kéo theo của hai mệnh đề P,Q. Kí hiệu P → Q. P được gọi là giả thiết và Q được gọi là kết luận.
Ví dụ : Cho hai mệnh đề P và Q như sau
P = " tam giác T là đều "
Q = " tam giác T có một góc bằng 60°"
Để xét chân trị của mệnh đề P → Q, ta có nhận xét sau :
- Nếu P đúng, nghĩa là tam giác T là đều thì rõ ràng rằng P → Q là đúng.
- Nếu P sai, nghĩa là tam giác T không đều và cũng không là cân thì dù Q là đúng hay sai thì mệnh đề P → Q vẫn đúng.
Sau đây là bảng chân trị của ví dụ và cũng là bảng chân trị của mệnh đề P →Q.
Qui tắc : mệnh đề kéo theo chỉ sai khi giả thiết đúng và kết luận sai. Các trường hợp khác là đúng.
Từ mệnh đề P → Q, chúng ta có thể tạo ra các mệnh đề kéo theo khác như là mệnh đề Q → P và ¬ Q → P được gọi là mệnh đề đảo và mệnh đề phản đảo của mệnh đề P → Q.
Ví dụ : Tìm mệnh đề đảo và phản đảo của mệnh đề sau
" Nếu tôi có nhiều tiền thì tôi mua xe hơi"
Mệnh đề đảo là :
" Nếu tôi mua xe hơi thì tôi có nhiều tiền"
Mệnh đề phản đảo là :
" Nếu tôi không mua xe hơi thì tôi không có nhiều tiền"
Phép tương đương (BICONDITIONAL)
Cho P và Q là hai mệnh đề. Câu "P nếu và chỉ nếu Q" là một mệnh đề mới được gọi là P tương đương Q. Kí hiệu P Q. Mệnh đề tương đương là đúng khi P và Q có cùng chân trị.
P Q = (P → Q) ^ (Q → P)
Đọc là : P nếu và chỉ nếu Q
P là cần và đủ đối với Q
Nếu P thì Q và ngược lại
Bảng chân trị
p q p ↔q
T T T
T F F
F T F
F F T
Biểu thức mệnh đề (LOGICAL CONNECTIVES)
Cho P, Q, R,... là các mệnh đề. Nếu các mệnh đề này liên kết với nhau bằng các phép toán thì ta được một biểu thức mệnh đề.
Chú ý : . Một mệnh đề cũng là một biểu thức mệnh đề
. Nếu P là một biểu thức mệnh đề thì P cũng là biểu thức mệnh đề
Chân trị của biểu thức mệnh đề là kết quả nhận được từ sự kết hợp giữa các phép toán và chân trị của các biến mệnh đề.
Ví dụ : Tìm chân trị của biểu thức mệnh đề ¬ P ^V (Q ^ R )
Do biểu thức mệnh đề là sự liên kết của nhiều mệnh đề bằng các phép toán nên chúng ta có thể phân tích để biểu diễn các biểu thức mệnh đề này bằng một cây mệnh đề.
Ví dụ : Xét câu phát biểu sau :
" Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả."
Đây là một biểu thức mệnh đề và phép toán chính là phép hội. Có thể viết lại như sau :
"Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có.
Nhưng,
nếu cô ta không thắng thì cô ta sẽ mất tất cả. "
Cả hai mệnh đề chính trong biểu thức mệnh đề này là mệnh đề phức hợp. Có thể định nghĩa các biến mệnh đề như sau:
P: Michelle thắng trong kỳ thi Olympic
Q: mọi người sẽ khâm phục cô ấy
R: cô ta sẽ trở nên giàu có
S: cô ta sẽ mất tất cả
Biểu diễn câu phát biểu trên bằng các mệnh đề và các phép toán, ta có biểu thức mệnh đề sau : ( P → (Q ^ R)) ^ ( ¬ P → S)
Biểu diễn câu phát biểu trên thành một cây ngữ nghĩa như sau :
Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả. Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nếu cô ta không thắng thì cô ta sẽ mất tất cả. AND Michelle thắng trong kỳ thi Olympic Mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Cô ta không thắng Cô ta sẽ mất tất cả. Mọi người sẽ khâm phục cô ấy Cô ta sẽ trở nên giàu có. Cô ta sẽ mất tất cả. AND NOT
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
bài tập chứng minh tương đương( đã chỉnh sửa)
levanhung 23/2/2017, 20:49
levanhung đã viết: Để chứng minh hai biểu thức : r ٨¬s →¬ q ≡ q→ ¬r ٧ s
*Ta có hai cách:
* CÁCH 1: Ta chứng minh hai biểu thức tương đương vs nhau bằng bảng sự thật:
Ta đã chứng minh xong! Đó là cách 1
*CÁCH 2
Vận dụng các luật và nhưng tương đương đã biết để biến đổi mệnh đề logic phức hợp sang tương dương giống nó. trước hết cần chứng minh sự tương đương sau:
p → q ≡ ¬q→ ¬p ( kéo theo tương đương vs phản đảo của nó)
Admin: Đây không phải là Luật De Morgan!
đầu tiên chứng minh biểu thức trên bằng bảng sự thật:
Ta đã chứng minh được biểu thức trên tương đương
Tiếp theo:
Áp dụng định luật De Mocgan để đưa biểu thức ban đầu về dạng cần tương đương vs nó:
¬¬q→ ¬(r ٨¬s)
≡ q → ¬(r ٨ ¬s)
phủ định của hội bằng tuyển các phủ định
=> q → ( ¬r ٧¬¬s)
≡ q → ( ¬r ٧s )≡ ¬q → (r ٧ ¬s)
Giải thích:
Vì "Phủ định của hội bằng tuyển các phủ định" nên ta có cách chuyển đổi như trên.
Admin:
- Rất cố gắng. Quan trọng là bằng sức của mình (thấy rõ)
- "Phủ định của một hội bằng tuyển các phủ định" mới là Luật De Morgan: ¬(p ٨ q) ≡ (¬p ٧ ¬q)
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
Re: Chương 1: Logic - Tập hợp
NgoTrungHieu16050054 24/2/2017, 15:21
( r Ʌ ¬s ) → ¬q ≡ q → (¬r V s )
BT1: Nếu bạn cao dưới 1.5m và bạn không trên 18 tuổi thì bạn không được lái xe.
BT2:Nếu bạn được lái xe thì bạn phải không cao dưới 1.5m " HOẶC" bạn trên 18 tuổi
BT2 có vẻ hơi không hợp lý khi dùng phép tuyển (HOẶC) .
xin thầy và các bạn cho ý kiến
BT1: Nếu bạn cao dưới 1.5m và bạn không trên 18 tuổi thì bạn không được lái xe.
BT2:Nếu bạn được lái xe thì bạn phải không cao dưới 1.5m " HOẶC" bạn trên 18 tuổi
BT2 có vẻ hơi không hợp lý khi dùng phép tuyển (HOẶC) .
xin thầy và các bạn cho ý kiến
NgoTrungHieu16050054- Tổng số bài gửi : 1
Join date : 22/02/2017
đóng góp ý kiến cho bạn Trung Hiếu
levanhung 26/2/2017, 10:17
[size=14]BT2:Nếu bạn được lái xe thì bạn phải không cao dưới 1.5m " HOẶC" bạn trên 18 tuổi
Trả lời: theo ý kiến riêng của mình thì từ “HOẶC” ở đây có nghĩa là: bạn phải trên 1.5m hoặc là bạn trên 18 tuổi thì mới đủ điều kiện trên thì bạn mới được lái xe máy
Trả lời: theo ý kiến riêng của mình thì từ “HOẶC” ở đây có nghĩa là: bạn phải trên 1.5m hoặc là bạn trên 18 tuổi thì mới đủ điều kiện trên thì bạn mới được lái xe máy
Và mình còn đọc được một số tài liệu trên mang như thế này:
Phép tuyển.
[/size]Hai phán đoán đơn P, Q, có thể liên kết với nhau bằng liên từ lôgíc “HOẶC” lập thành một nhóm phán đoán phức. Phán đoán này được gọi là tuyển của hai phán đoán P, Q. Do liên từ HOẶC trong ngôn ngữ tự nhiên có hai nghĩa : HOẶC có nghĩa HAY LÀ, VỪA LÀ, HOẶC còn có nghĩa HOẶC LÀ, HOẶC LÀ. Ở nghĩa này liên từ HOẶC có tính chất lựa chọn dứt khoát. Chính vì vậy mà phép tuyển cũng có hai mức độ : Phép tuyển thường và phép tuyển chặt
Bạn xem xem có thể giải quyết được thắc mắc của bạn chưa nhé!
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
Re: Chương 1: Logic - Tập hợp
huynhleanhtuank19 1/3/2017, 11:39
Tên tiếng anh của các dấu ngoặc....
‘ ‘ dấu trích dẫn đơn = single quotation mark
” ” dấu trích dẫn kép = double quotation marks
( ) dấu ngoặc = parenthesis (hoặc ‘brackets’)
[ ] dấu ngoặc vuông = square brackets
& dấu và= ampersand
‘ ‘ dấu trích dẫn đơn = single quotation mark
” ” dấu trích dẫn kép = double quotation marks
( ) dấu ngoặc = parenthesis (hoặc ‘brackets’)
[ ] dấu ngoặc vuông = square brackets
& dấu và= ampersand
huynhleanhtuank19- Tổng số bài gửi : 3
Join date : 21/02/2017
Các Dấu Ngoặc Thông Dụng Trong Toán Học Rời Rạc, Cũng Như Trong Lập Trình.
nguyenhuuduc08(k19) 1/3/2017, 11:44
- ( ) : Dấu Ngoặc Đơn (Parentheses)
Vd: (1,2,3)
- [ ] : Dấu Ngoặc Vuông (Square brackets)
Vd: [1,2,3]
- < > : Dấu Ngoặc Nhọn (Curly brackets)
Vd: <1,2,3>
- { } : Dấu Ngoặc Móc (Braces)
Vd: {1,2,3}
- ' ' : Dấu Nháy Đơn (Apostrophe)
Vd: 'x,y,z'
- " " : Dấu Nháy Kép (Quotation marks)
Vd: "x,y,z"
Vd: (1,2,3)
- [ ] : Dấu Ngoặc Vuông (Square brackets)
Vd: [1,2,3]
- < > : Dấu Ngoặc Nhọn (Curly brackets)
Vd: <1,2,3>
- { } : Dấu Ngoặc Móc (Braces)
Vd: {1,2,3}
- ' ' : Dấu Nháy Đơn (Apostrophe)
Vd: 'x,y,z'
- " " : Dấu Nháy Kép (Quotation marks)
Vd: "x,y,z"
nguyenhuuduc08(k19)- Tổng số bài gửi : 4
Join date : 17/02/2017
Hình trình bày tập hợp lũy thừa của tập hợp S={a,b,c,d}
PhanTanSangK19 1/3/2017, 12:35
Nhắc lại lý thuyết:Tập hợp lũy thừa là tập hợp của một tập hợp A là tập hợp chứa tất cả các tập hợp con của tập hợp A.
Kí hiệu p(A), ℘(A), 2^A .
Giải:
Tập lũy thừa của tập hợp A (a,b,c,d) là tập hợp P(A) chứa tất cả các tập hợp con của A.
Vậy ta có:
P(A) = { {Ø} , {a} , {b} , {c} , {d} , {a,b} , {a,c} , {a,d} , {b,c} , {b,d} , {c,d} , {a,b,c} , {a,b,d} , {a,c,d} , {b,c,d} , {a,b,c,d} }
Kí hiệu p(A), ℘(A), 2^A .
Giải:
Tập lũy thừa của tập hợp A (a,b,c,d) là tập hợp P(A) chứa tất cả các tập hợp con của A.
Vậy ta có:
P(A) = { {Ø} , {a} , {b} , {c} , {d} , {a,b} , {a,c} , {a,d} , {b,c} , {b,d} , {c,d} , {a,b,c} , {a,b,d} , {a,c,d} , {b,c,d} , {a,b,c,d} }
Được sửa bởi PhanTanSangK19 ngày 3/3/2017, 02:19; sửa lần 1.
PhanTanSangK19- Tổng số bài gửi : 10
Join date : 16/02/2017
trình bày tập lũy thừa
levanhung 2/3/2017, 21:51
Tập hợp lũy thừa S là tất cả các tập con có tâp hợp S đó, và đk kí hiệu là P(S)
Giải bài tập: hãy trình bày tập lũy thừa của tập hợp S={a,b,,c,d}
Giải
Tập lũy thừa của n phàn tử có số tập hợp con được tính theo công thức là: 2˄n
Vậy tập lũy thừa của tập S là: 2˄4=16
Vậy S có 16 tập con
S={(Ø),(a),(b),(c),(d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(a,b,c),(a,c,d),(b,c,d),(a,b,d),(a,b,c,d)}
XONG
Giải bài tập: hãy trình bày tập lũy thừa của tập hợp S={a,b,,c,d}
Giải
Tập lũy thừa của n phàn tử có số tập hợp con được tính theo công thức là: 2˄n
Vậy tập lũy thừa của tập S là: 2˄4=16
Vậy S có 16 tập con
S={(Ø),(a),(b),(c),(d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(a,b,c),(a,c,d),(b,c,d),(a,b,d),(a,b,c,d)}
XONG
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
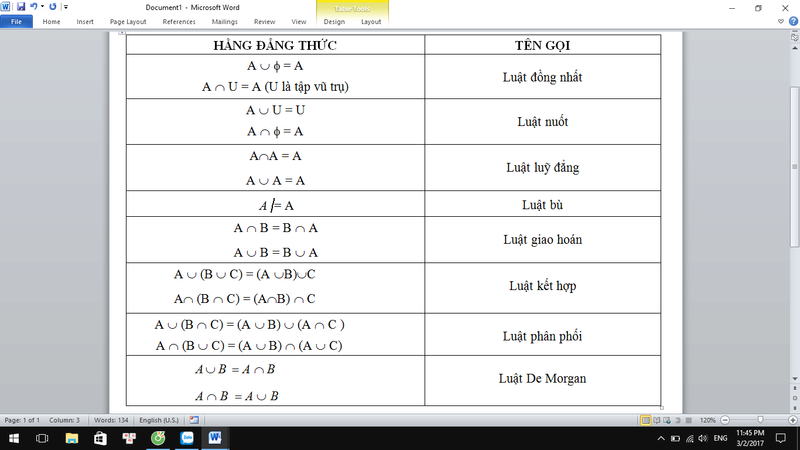[/color]
Nguyễn Hoàng Phi K19- Tổng số bài gửi : 4
Join date : 19/02/2017
Age : 26
Đến từ : Bình Phước
Các Phép Tính Mệnh Đề
Nguyễn Hoàng Phi K19 3/3/2017, 00:03
Các phép tính mệnh đề
Trong phép tính mệnh đề, người ta không quan tâm đến ý nghĩa của câu phát biểu mà chỉ chú ý đến chân trị của các mệnh đề. Do đó, khi thực hiện các phép toán mệnh đề thông thường người ta không ghi rõ các câu phát biểu mà chỉ ghi ký hiệu. Các chữ cái sẽ được dùng để ký hiệu các mệnh đề. Những chữ cái thường dùng là P, Q, R,.....
Mệnh đề chỉ có một giá trị đơn (luôn đúng hoặc sai) được gọi là mệnh đề nguyên từ ( atomic proposition ). Các mệnh đề không phải là mệnh đề nguyên từ được gọi là mệng đề phức hợp (compound propositions). Thông thường, tất cả mệnh đề phức hợp là mệnh đề liên kết (có chứa phép tính mệnh đề).
Các phép tính mệnh đề được sử dụng nhằm mục đích kết nối các mệnh đề lại với nhau tạo ra một mệnh đề mới. Các phép toán mệnh đề được trình bày trong chương này bao gồm : phép phủ định, phép hội, phép tuyển, phép XOR, phép kéo theo, phép tương đương.
Phép phủ định (NEGATION)
Cho P là một mệnh đề, câu "không phải là P" là một mệnh đề khác được gọi là phủ định của mệnh đề P. Kí hiệu : ¬ P (
¯
P
).
Ví dụ : P = " 2 > 0 "
¬ P = " 2 ≤ 0 "
Bảng chân trị (truth table)
p ¬ p
T F
F T
Qui tắc: Nếu P có giá trị là T thì phủ định P có giá trị là F.
Phép hội (CONJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P và Q" là một mệnh đề mới được gọi là hội của 2 mệnh đề P và Q. Kí hiệu P ^ Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P ^ Q = " 2> 0 và 2 = 0 " là mệnh đề sai.
Bảng chân trị
p q p^q
T T T
T F F
F T F
F F F
Qui tắc : Hội của 2 mệnh đề chỉ đúng khi cả hai mệnh đề là đúng. Các trường hợp còn lại là sai.
Phép tuyển (DISJUNCTION)
Cho hai mệnh đề P, Q. Câu xác định "P hay (hoặc) Q" là một mệnh đề mới được gọi là tuyển của 2 mệnh đề P và Q. Kí hiệu P V Q.
Ví dụ : Cho 2 mệnh đề P và Q như sau
P = " 2 > 0 " là mệnh đề đúng
Q = " 2 = 0 " là mệnh đề sai
P V Q = " 2 ≥ 0 " là mệnh đề đúng.
p q pvq
T T T
T F T
F T T
F F F
Bảng chân trị
Qui tắc : Tuyển của 2 mệnh đề chỉ sai khi cả hai mệnh đề là sai. Các trường hợp còn lại là đúng.
Phép XOR
Cho hai mệnh đề P và Q. Câu xác định "loại trừ P hoặc lọai trừ Q", nghĩa là "hoặc là P đúng hoặc Q đúng nhưng không đồng thời cả hai là đúng" là một mệnh đề mới được gọi là P xor Q. Kí hiệu P ⊕ Q.
Bảng chân trị
p q p ⊕q
T T F
T F T
F T T
F F F
Phép toán trên bit
Các máy tính dùng các bit để biểu diễn thông tin. Một bit có 2 giá trị khả dĩ là 0 và 1. Bit cũng có thể được dùng để biểu diễn chân trị. Thường người ta dùng bit 1 để biểu diễn chân trị đúng và bit 0 để biểu diễn chân trị sai. Các phép toán trên bit trong máy tính là các phép toán logic. Thông tin thường được biển diễn bằng cách dùng các xâu bit. Ta có định nghĩa xâu bit như sau:
Định nghĩa : Một xâu bit (hoặc xâu nhị phân) là dãy có một hoặc nhiều bit. Chiều dài của xâu là số các bit trong xâu đó.
Ví dụ : 101011000 là một xâu bit có chiều dài là 9
Có thể mở rộng các phép toán trên bit tới các xâu bit. Người ta định nghĩa các OR bit, AND bit và XOR bit đối với 2 xâu bit có cùng chiều dài là các xâu có các bit của chúng là ca1c OR, AND, XOR của các bit tương ứng trong 2 xâu tương ứng. Chúng ta cũng dùng các kí hiệu ^, v, ⊕ để biểu diễn các phép tính OR bit, AND và XOR tương ứng.
Ví dụ : Tìm OR bit, AND bit và XOR bit đối với 2 xâu sau đây (mỗi xâu được tách thành 2 khối, mỗi khối có 5 bit cho dễ đọc)
01101 10110
11000 11101
11101 11111 OR bit
01000 10100 AND bit
10101 01011 XOR bit
Phép kéo theo (IMPLICATION)
Cho P và Q là hai mệnh đề. Câu "Nếu P thì Q" là một mệnh đề mới được gọi là mệnh đề kéo theo của hai mệnh đề P,Q. Kí hiệu P → Q. P được gọi là giả thiết và Q được gọi là kết luận.
Ví dụ : Cho hai mệnh đề P và Q như sau
P = " tam giác T là đều "
Q = " tam giác T có một góc bằng 60°"
Để xét chân trị của mệnh đề P → Q, ta có nhận xét sau :
- Nếu P đúng, nghĩa là tam giác T là đều thì rõ ràng rằng P → Q là đúng.
- Nếu P sai, nghĩa là tam giác T không đều và cũng không là cân thì dù Q là đúng hay sai thì mệnh đề P → Q vẫn đúng.
Sau đây là bảng chân trị của ví dụ và cũng là bảng chân trị của mệnh đề P →Q.
Qui tắc : mệnh đề kéo theo chỉ sai khi giả thiết đúng và kết luận sai. Các trường hợp khác là đúng.
Từ mệnh đề P → Q, chúng ta có thể tạo ra các mệnh đề kéo theo khác như là mệnh đề Q → P và ¬ Q → P được gọi là mệnh đề đảo và mệnh đề phản đảo của mệnh đề P → Q.
Ví dụ : Tìm mệnh đề đảo và phản đảo của mệnh đề sau
" Nếu tôi có nhiều tiền thì tôi mua xe hơi"
Mệnh đề đảo là :
" Nếu tôi mua xe hơi thì tôi có nhiều tiền"
Mệnh đề phản đảo là :
" Nếu tôi không mua xe hơi thì tôi không có nhiều tiền"
Phép tương đương (BICONDITIONAL)
Cho P và Q là hai mệnh đề. Câu "P nếu và chỉ nếu Q" là một mệnh đề mới được gọi là P tương đương Q. Kí hiệu P Q. Mệnh đề tương đương là đúng khi P và Q có cùng chân trị.
P Q = (P → Q) ^ (Q → P)
Đọc là : P nếu và chỉ nếu Q
P là cần và đủ đối với Q
Nếu P thì Q và ngược lại
Bảng chân trị
p q p ↔q
T T T
T F F
F T F
F F T
Biểu thức mệnh đề (LOGICAL CONNECTIVES)
Cho P, Q, R,... là các mệnh đề. Nếu các mệnh đề này liên kết với nhau bằng các phép toán thì ta được một biểu thức mệnh đề.
Chú ý : . Một mệnh đề cũng là một biểu thức mệnh đề
. Nếu P là một biểu thức mệnh đề thì P cũng là biểu thức mệnh đề
Chân trị của biểu thức mệnh đề là kết quả nhận được từ sự kết hợp giữa các phép toán và chân trị của các biến mệnh đề.
Ví dụ : Tìm chân trị của biểu thức mệnh đề ¬ P ^V (Q ^ R )
Do biểu thức mệnh đề là sự liên kết của nhiều mệnh đề bằng các phép toán nên chúng ta có thể phân tích để biểu diễn các biểu thức mệnh đề này bằng một cây mệnh đề.
Ví dụ : Xét câu phát biểu sau :
" Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả."
Đây là một biểu thức mệnh đề và phép toán chính là phép hội. Có thể viết lại như sau :
"Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có.
Nhưng,
nếu cô ta không thắng thì cô ta sẽ mất tất cả. "
Cả hai mệnh đề chính trong biểu thức mệnh đề này là mệnh đề phức hợp. Có thể định nghĩa các biến mệnh đề như sau:
P: Michelle thắng trong kỳ thi Olympic
Q: mọi người sẽ khâm phục cô ấy
R: cô ta sẽ trở nên giàu có
S: cô ta sẽ mất tất cả
Biểu diễn câu phát biểu trên bằng các mệnh đề và các phép toán, ta có biểu thức mệnh đề sau : ( P → (Q ^ R)) ^ ( ¬ P → S)
Biểu diễn câu phát biểu trên thành một cây ngữ nghĩa như sau :
Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nhưng, nếu cô ta không thắng thì cô ta sẽ mất tất cả. Nếu Michelle thắng trong kỳ thi Olympic, mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Nếu cô ta không thắng thì cô ta sẽ mất tất cả. AND Michelle thắng trong kỳ thi Olympic Mọi người sẽ khâm phục cô ấy, và cô ta sẽ trở nên giàu có. Cô ta không thắng Cô ta sẽ mất tất cả. Mọi người sẽ khâm phục cô ấy Cô ta sẽ trở nên giàu có. Cô ta sẽ mất tất cả. AND NOT
Nguyễn Hoàng Phi K19- Tổng số bài gửi : 4
Join date : 19/02/2017
Age : 26
Đến từ : Bình Phước
Chuyển văn bản TCVN3 sang văn bản Unicode bằng Unikey
PhanTanSangK19 8/3/2017, 13:00
Bước 1: Mở file văn bản TCVN3 cần chuyển sang Unicode (có thể dùng MS Word).
Bước 2: Bôi đen nội dung văn bản cần chuyển, hoặc nhấn tổ hợp Ctrl+A để bôi đen tất cả văn bản, rồi Ctrl+C hoặc Ctrl+X để lưu văn bản vào clipboard.
Bước 3: Mở công cụ đổi mã của Unikey bằng cách click chuột phải vào icon Unikey (Góc phải thanh taskbar) và chọn "Công cụ...". Để thao tác nhanh, ta có thể dùng tổ hợp Ctrl + Shift +F6.
Bước 4: Sau khi cửa sổ Unikey Toolkit xuất hiện:
- Chọn bảng mã cho file nguồn là TCVN3.
-Chọn bảng mã đích là Unicode.
-Click vào Chuyển mã.
Bước 5: Ctrl+V lên trang trắng trong MS Word để dán văn bản đã được chuyển mã thành công vào văn bản, chỉnh sửa bố cục và Save.
________________________________________________________________________________________
Bước 2: Bôi đen nội dung văn bản cần chuyển, hoặc nhấn tổ hợp Ctrl+A để bôi đen tất cả văn bản, rồi Ctrl+C hoặc Ctrl+X để lưu văn bản vào clipboard.
Bước 3: Mở công cụ đổi mã của Unikey bằng cách click chuột phải vào icon Unikey (Góc phải thanh taskbar) và chọn "Công cụ...". Để thao tác nhanh, ta có thể dùng tổ hợp Ctrl + Shift +F6.
Bước 4: Sau khi cửa sổ Unikey Toolkit xuất hiện:
- Chọn bảng mã cho file nguồn là TCVN3.
-Chọn bảng mã đích là Unicode.
-Click vào Chuyển mã.
Bước 5: Ctrl+V lên trang trắng trong MS Word để dán văn bản đã được chuyển mã thành công vào văn bản, chỉnh sửa bố cục và Save.
________________________________________________________________________________________
PhanTanSangK19- Tổng số bài gửi : 10
Join date : 16/02/2017
cách chuyển văn bản từ TCVN3 sang Unicode
levanhung 8/3/2017, 20:52
Bước 1: ta bôi đen và copy văn bản được gõ bằng TCVN3.
Bước 2: ta nhấp chuột trái vào biểu tượng chữ V của Unikey ở góc trái màn hình, chọn như trong hình.
Bước 3: chọn nguồn là TCVN3 và chọn đích là Unicode. Sau đó nhấp vào “Chuyển mã”
(làm tương tự với từ Unicode sang TCVN3).
Bước 4: chọn OK và đóng lại.
Bước 5: Paste văn bản ra màn hình.
Bước 2: ta nhấp chuột trái vào biểu tượng chữ V của Unikey ở góc trái màn hình, chọn như trong hình.
Bước 3: chọn nguồn là TCVN3 và chọn đích là Unicode. Sau đó nhấp vào “Chuyển mã”
(làm tương tự với từ Unicode sang TCVN3).
Bước 4: chọn OK và đóng lại.
Bước 5: Paste văn bản ra màn hình.
levanhung- Tổng số bài gửi : 11
Join date : 21/02/2017
Re: Chương 1: Logic - Tập hợp
nguyenthiha047(k19) 10/3/2017, 21:55
Chuyển font chữ từ Unicode sang TCVN3 và ngược lại
Bước 1:
Khởi động Unikey sau đó nhấn đồng thời Ctrl + Shift + F6 sẽ hiện ra một bảng chọn cho phép chuyển đổi giữa Mã TCVN3(VnTime) sang Unicode(Times New Roman) và ngược lại. (như hình)
Bước 2:
– Tại ô số 1: (khoanh đỏ) chọn định dạng mã văn bản nguồn của máy
– Tại ô số 2: chọn định dạng mã mà mình muốn chuyển đổi văn bản của mình sang.
– Ô số 3: là nút hoán đổi nội dung 2 ô số 1 và 2, có thể dùng thử (click chuột 2 lần vào đó thì trở lại trạng thái như chưa click)
Bước 3:
– Mở văn bản mình muốn chuyển
– Copy đoạn văn bản muốn chuyển vào clipboard
-Đánh dấu vào ô ố 4 như hình trên
Bước 4:
– Click chuột 1 lần vào nút Convert(chuyển đổi) ở vùng khoanh số 5.
– Chọn vị trí mình muốn dán văn bản sau khi đã chuyển đổi vào và nhấn đồng thời tổ hợp phímCtrl + V để dán văn bản từ clipdoard ra.
Kiểm tra lại đoạn văn bản và kết thúc.
Bước 1:
Khởi động Unikey sau đó nhấn đồng thời Ctrl + Shift + F6 sẽ hiện ra một bảng chọn cho phép chuyển đổi giữa Mã TCVN3(VnTime) sang Unicode(Times New Roman) và ngược lại. (như hình)
Bước 2:
– Tại ô số 1: (khoanh đỏ) chọn định dạng mã văn bản nguồn của máy
– Tại ô số 2: chọn định dạng mã mà mình muốn chuyển đổi văn bản của mình sang.
– Ô số 3: là nút hoán đổi nội dung 2 ô số 1 và 2, có thể dùng thử (click chuột 2 lần vào đó thì trở lại trạng thái như chưa click)
Bước 3:
– Mở văn bản mình muốn chuyển
– Copy đoạn văn bản muốn chuyển vào clipboard
-Đánh dấu vào ô ố 4 như hình trên
Bước 4:
– Click chuột 1 lần vào nút Convert(chuyển đổi) ở vùng khoanh số 5.
– Chọn vị trí mình muốn dán văn bản sau khi đã chuyển đổi vào và nhấn đồng thời tổ hợp phímCtrl + V để dán văn bản từ clipdoard ra.
Kiểm tra lại đoạn văn bản và kết thúc.
nguyenthiha047(k19)- Tổng số bài gửi : 4
Join date : 17/02/2017
Định luật suy ra từ định luật De Morgan
PhanTanSangK19 11/4/2017, 17:15
Như đã biết thì định luật De Morgan là "Phủ định của một hội bằng tuyển các phủ định" :
¬(p ٨ q) ≡ (¬p ٧ ¬q).
Vậy Phủ định của một tuyển bằng hội các phủ định thì sao ?
Như đã chứng minh ở trên thì ngoài định luật De Morgan thì ta còn có định luật ngược đó là Phủ định của một tuyển bằng hội các phủ định : ¬(p ٧ q) ≡ (¬p ٨ ¬q) .
¬(p ٨ q) ≡ (¬p ٧ ¬q).
Vậy Phủ định của một tuyển bằng hội các phủ định thì sao ?
Như đã chứng minh ở trên thì ngoài định luật De Morgan thì ta còn có định luật ngược đó là Phủ định của một tuyển bằng hội các phủ định : ¬(p ٧ q) ≡ (¬p ٨ ¬q) .
PhanTanSangK19- Tổng số bài gửi : 10
Join date : 16/02/2017
Similar topics» Địa chỉ Logic và địa chỉ Vật lý
» Thảo luận Bài 8
» bài tập phân đoạn, tính địa chỉ vật lý cho địa chỉ logic
» Thảo luận Bài 1
» Thảo luận Bài 3
» Thảo luận Bài 8
» bài tập phân đoạn, tính địa chỉ vật lý cho địa chỉ logic
» Thảo luận Bài 1
» Thảo luận Bài 3
Trang 1 trong tổng số 1 trang
Permissions in this forum:
Bạn không có quyền trả lời bài viết